Заполни пропуски в таблице, выполнив вычисления.
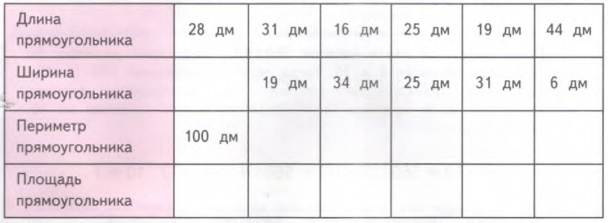
Сравни результаты в третьей и четвертой строках таблицы. Какой вывод можно сделать? При каких размерах прямоугольник имеет наибольшую площадь? Как называется такой прямоугольник?

1 столбик:
100 : 2 − 28 = 50 − 28 = 22 (дм) − ширина прямоугольника;
28 * 22 = 616 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 28, y: 22}$
2 столбик:
(31 + 19) * 2 = 50 * 2 = 100 (дм) − периметр прямоугольника;
31 * 19 = 589 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 31, y: 19}$
3 столбик:
(16 + 34) * 2 = 50 * 2 = 100 (дм) − периметр прямоугольника;
16 * 34 = 544 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 16, y: 34}$
4 столбик:
(25 + 25) * 2 = 50 * 2 = 100 (дм) − периметр прямоугольника;
25 * 25 = 625 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 25, y: 25}$
5 столбик:
(19 + 31) * 2 = 100 (дм) − периметр прямоугольника;
19 * 31 = 589 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 19, y: 31}$
6 столбик:
(44 + 6) * 2 = 100 (дм) − периметр прямоугольника;
44 * 6 = 264 $(дм^2)$ − площадь прямоугольника.
$\snippet{name: column_multiplication, x: 44, y: 6}$
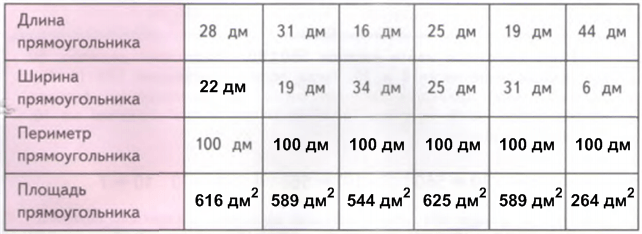
Периметры прямоугольников равны.
Наибольшая площадь у квадрата, стороны которого равны 25 дм.