1) Рассмотри чертеж и выпиши названия всех многоугольников.
2) Запиши обозначения равнобедренных треугольников; разносторонних треугольников.
3) Запиши обозначения всех прямых углов на чертеже. Есть ли на чертеже квадраты? прямоугольники?
4) Найди периметр и площадь квадрата ABCD и прямоугольника ABKM.
5) Сравни площадь прямоугольника ABKM и площадь треугольника ACM.
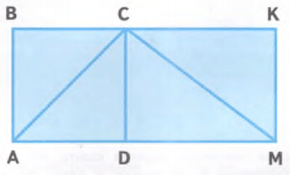
Многоугольники:
ABKM, ABC, ACD, CDM, CKM, ABCD, CKMD, ACM, ABCM, ACKM.
Равнобедренные треугольники:
ΔABC и ΔACD − так как ABCD − квадрат деленный диагональю.
Разносторонние треугольники:
ΔCDM, ΔCKM, ΔACM.
Прямые углы:
∠ABC, ∠BCD, ∠ADC, ∠DAB, ∠CKM, ∠CDM, ∠DCK, ∠DMK.
Квадрат:
ABCD.
Прямоугольники: DCKM, ABKM.
Так как у квадрата все стороны равны, то:
AB = BC = CD = AD = 3 см.
Найдем периметр квадрата:
3 * 4 = 12 (см);
Найдем площадь квадрата:
3 * 3 = 9 ($см^2$).
Запишем длины сторон прямоугольника ABKM:
AB = KM = 3 (см) − ширина прямоугольника;
BK = AM = 7 (см) − длина прямоугольника.
Найдем периметр прямоугольника:
(3 + 7) * 2 = 10 * 2 = 20 (см).
Найдем площадь прямоугольника:
3 * 7 = 21 ($см^2$).
Площадь прямоугольника ABKM = 21 ($см^2$);
Площадь треугольника ACD = ABCD : 2 = 9 : 2 = 4 $см^2$ 50 $мм^2$;
Площадь прямоугольника DCKM = ABKM − ABCD = 21 − 9 = 12 ($см^2$), значит площадь треугольника CDM = DCKM : 2 = 12 : 2 = 6 ($см^2$).
Следовательно, площадь треугольника ACM = 4 $см^2$ 50 $мм^2$ + 6 $см^2$ = 10 $см^2$ 50 $мм^2$.
Площадь прямоугольника ABKM больше площади треугольника ACM в:
21 $см^2$ : 10 $см^2$ 50 $мм^2$ = 2100 : 1050 = 2 (раза).
Посмотреть калькулятор Вычисления в столбик