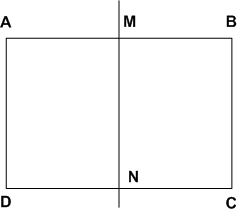
Решение: Возьмем прямоугольник ABCD и проведем через его центр симметрии прямую. Раз прямая проведена через центр симметрии то получается, что точка A симметрична точке B относительно точки M, а точка D симметрична точке C относительно точки N, следовательно: AM = MB; DN = NC. Таким образом если прямоугольник AMND развернуть на 180 градусов относительно отрезка MN, то прямоугольник AMND совместится с прямоугольником MBCN и отсюда следует что прямоугольник AMND = прямоугольнику MBCN.