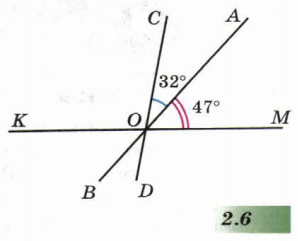
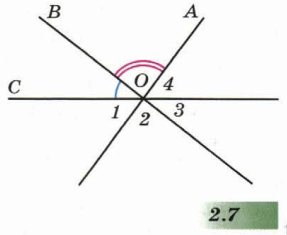
а) Прямые AB, CD, KM, пересекаются в точке O (рис.2.6), причем ∠AOM = 47° и ∠AOC = 32°. Найдите ∠COK, ∠KOB, ∠BOD, ∠DOM. б) Через точку O проведены три прямые (рис.2.7), ∠AOC = 130°, ∠AOB = 91°. Найдите углы, обозначенные цифрами 1, 2, 3, 4.

а) Прямые AB, CD, KM, пересекаются в точке O (рис.2.6), причем ∠AOM = 47° и ∠AOC = 32°. Найдите ∠COK, ∠KOB, ∠BOD, ∠DOM. б) Через точку O проведены три прямые (рис.2.7), ∠AOC = 130°, ∠AOB = 91°. Най...

Решение а

Дано: AB∩KM∩CD = O; ∠AOM = 47°; ∠AOC = 32°. Найти: ∠COK = ?; ∠KOB = ?; ∠BOD = ?; ∠DOM = ?. Решение: ∠COK + ∠AOC + ∠AOM = 180°; ∠COK = 180°− (∠AOC + ∠AOM); ∠COK = 180°− (32° + 47°) = 180° − 79° = 101°; ∠KOB = ∠AOM = 47° − вертикальные углы; ∠BOD = ∠AOC = 32° − вертикальные углы; ∠DOM = ∠COK = 101° − углы вертикальные. Ответ: ∠COK = 101°; ∠KOB = 47°; ∠BOD = 32°; ∠DOM = 101°.

Решение б

Дано: AO∩BO∩CO = O; ∠AOC = 130°; ∠AOB = 91°. Найти: ∠1 = ?; ∠2 = ?; ∠3 = ?; ∠4 = ?. Решение: ∠4 = 180° − ∠AOC; ∠4 = 180° − 130° = 50°; ∠1 = ∠4 = 50° − вертикальные углы; ∠2 = ∠AOB = 91° − вертикальные углы; ∠BOC = ∠AOC − ∠AOB; ∠BOC = 130° − 91° = 39°; ∠3 = ∠BOC = 39° − вертикальные углы. Ответ: ∠1 = 50°; ∠2 = 91°; ∠3 = 39°; ∠4 = 50°.