Постройте многоугольник, имеющий n сторон, если:
а) n = 4;
б) n = 5;
в) n = 6;
г) n = 7;
д) n = 8.
В каждом случае проведите все диагонали многоугольника. Объясните, почему число d всех диагоналей вычисляется по формуле d = $\frac{n(n-3)}{2}$.

Решение:
Диагональ многоугольника соединяет одну вершину треугольника с другой, кроме соседних, т.е. n − 3 точек, каждая диагональ соединяет 2 точки, поэтому среди диагоналей есть попарно совпадающие и поэтому количество диагоналей необходимо поделить на 2.
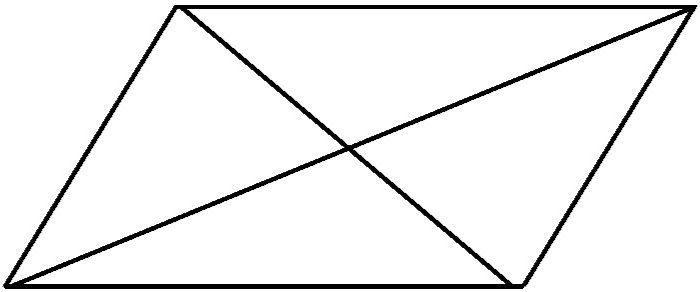
d = $\frac{n(n-3)}{2}$ = d = $\frac{4(4-3)}{2}$ = $\frac{4}{2}$ = 2 диагонали.
Ответ: 2 диагонали.
Решение:
Диагональ многоугольника соединяет одну вершину треугольника с другой, кроме соседних, т.е. n − 3 точек, каждая диагональ соединяет 2 точки, поэтому среди диагоналей есть попарно совпадающие и поэтому количество диагоналей необходимо поделить на 2.
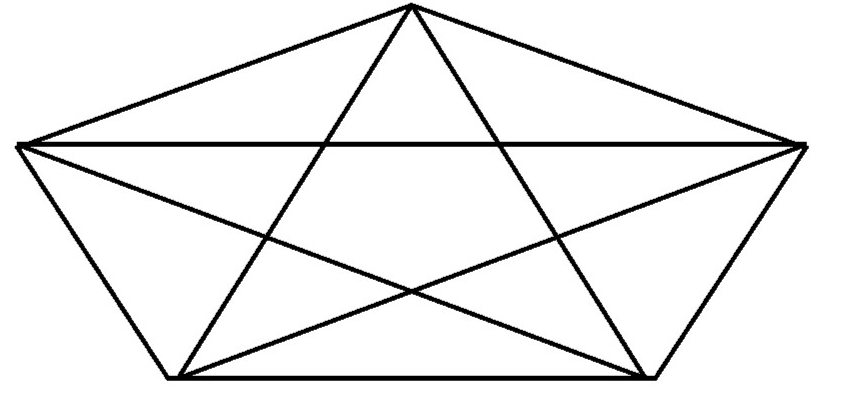
d = $\frac{n(n-3)}{2}$ = d = $\frac{5(5-3)}{2}$ = $\frac{10}{2}$ = 5 диагоналей.
Ответ: 5 диагоналей.
Решение:
Диагональ многоугольника соединяет одну вершину треугольника с другой, кроме соседних, т.е. n − 3 точек, каждая диагональ соединяет 2 точки, поэтому среди диагоналей есть попарно совпадающие и поэтому количество диагоналей необходимо поделить на 2.
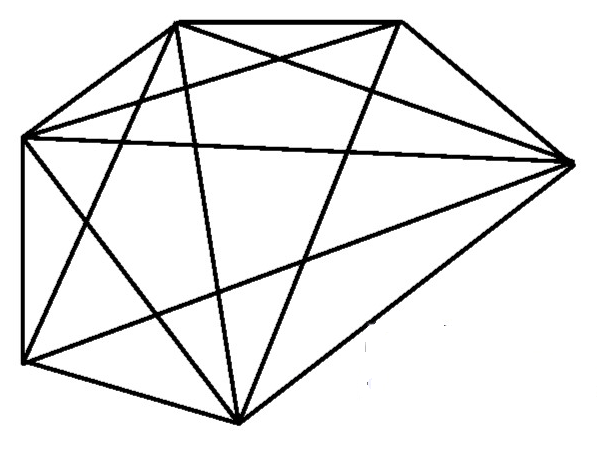
d = $\frac{n(n-3)}{2}$ = d = $\frac{6(6-3)}{2}$ = $\frac{18}{2}$ = 9 диагоналей.
Ответ: 9 диагоналей.
Решение:
Диагональ многоугольника соединяет одну вершину треугольника с другой, кроме соседних, т.е. n − 3 точек, каждая диагональ соединяет 2 точки, поэтому среди диагоналей есть попарно совпадающие и поэтому количество диагоналей необходимо поделить на 2.
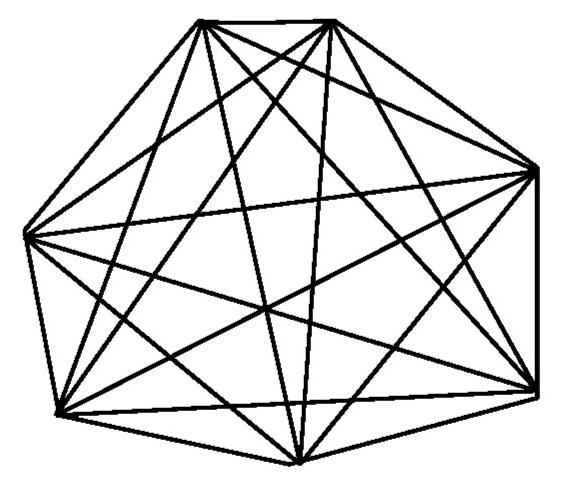
d = $\frac{n(n-3)}{2}$ = d = $\frac{7(7-3)}{2}$ = $\frac{28}{2}$ = 14 диагоналей.
Ответ: 14 диагоналей.
Решение:
Диагональ многоугольника соединяет одну вершину треугольника с другой, кроме соседних, т.е. n − 3 точек, каждая диагональ соединяет 2 точки, поэтому среди диагоналей есть попарно совпадающие и поэтому количество диагоналей необходимо поделить на 2.
d = $\frac{n(n-3)}{2}$ = d = $\frac{8(8-3)}{2}$ = $\frac{40}{2}$ = 20 диагоналей.
Ответ: 20 диагоналей.