(Для работы в парах). Используя графические представления, выясните, сколько решений имеет уравнение:
а) $\frac{k}{x} = x^2$, где k > 0;
б) $\frac{k}{x} = x^2$, где k < 0;
в) $\frac{k}{x} = x^3$, где k > 0;
г) $\frac{k}{x} = x^3$, где k < 0.
1) Распределите, кто выполняет задания а) и г), а кто − задания б) и в), и выполните их.
2) Проверьте друг у друга, верно ли построены графики функций $y = \frac{k}{x}$.
3) Обсудите правильность сделанных выводов о числе решений уравнения.

$\frac{k}{x} = x^2$, где k > 0
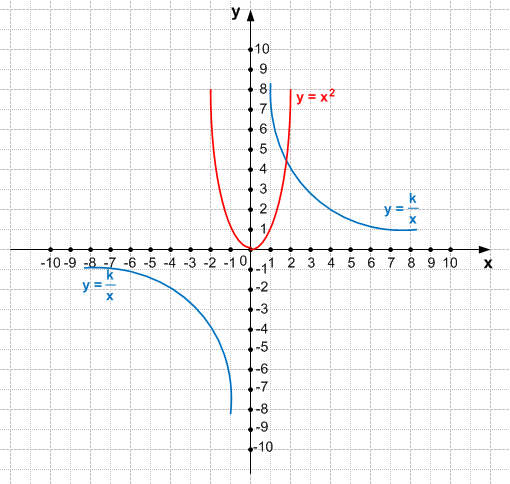
Уравнение имеет один корень.
$\frac{k}{x} = x^2$, где k < 0
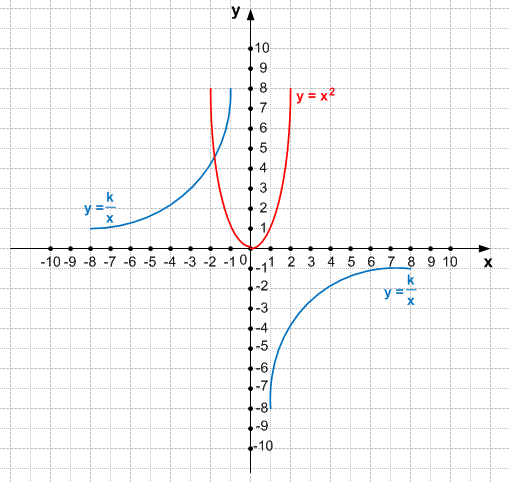
Уравнение имеет один корень.
$\frac{k}{x} = x^3$, где k > 0
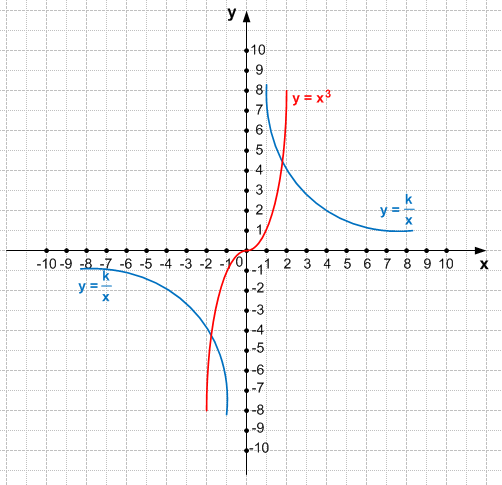
Уравнение имеет два корня.
$\frac{k}{x} = x^3$, где k < 0
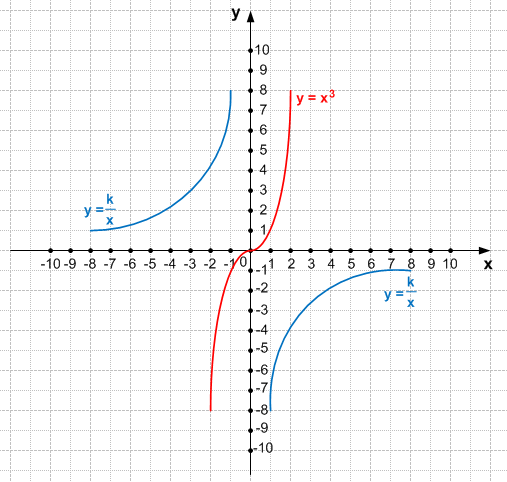
Уравнение не имеет корней.