1. Ответы
  2. 6 класс
  3. Математика
  4. #1485

Две равные фигуры наложили друг на друга (рис.24). Докажите, что площади закрашенных фигур равны.

6 классМатематика

Две равные фигуры наложили друг на друга (рис.24). Докажите, что площади закрашенных фигур равны.

Две равные фигуры наложили друг на друга (рис.24). Докажите, что площади закрашенных фигур равны.

Решение

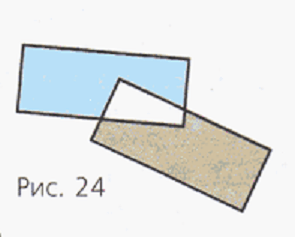
Решение: Допустим, что площадь голубой части равна S1, площадь серой части равна S2, площадь белой части равна S3, тогда: площадь первого прямоугольника равна S1 + S3; площадь второго прямоугольника равна S2 + S3. Так как по условию задачи прямоугольники равны, то: S1 + S3 = S2 + S3 S1 = S2 + S3 − S3 S1 = S2, то есть площади закрашенных фигур равны. Ответ: S1 = S2 − площади закрашенных фигур равны.